已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1,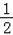 ).
).
(Ⅰ)求点P,Q的坐标;
(Ⅱ)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
解:(Ⅰ)∵y=x2﹣2x+1=(x﹣1)2
∴顶点P(1,0),
∵当x=0时,y=1,
∴Q(0,1),
(Ⅱ)①设抛物线C′的解析式为y=x2﹣2x+m,
∴Q′(0,m)其中m>1,
∴OQ′=m,
∵F(1,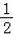 ),
),
过F作FH⊥OQ′,如图:
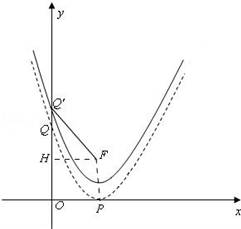
∴FH=1,Q′H=m﹣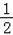 ,
,
在Rt△FQ′H中,FQ′2=(m﹣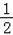 )2+1=m2﹣m+
)2+1=m2﹣m+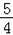 ,
,
∵FQ′=OQ′,
∴m2﹣m+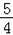 =m2,
=m2,
∴m=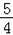 ,
,
∴抛物线C′的解析式为y=x2﹣2x+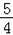 ,
,
②设点A(x0,y0),则y0=x02﹣2x0+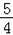 ,
,
过点A作x轴的垂线,与直线Q′F相交于点N,则可设N(x0,n),
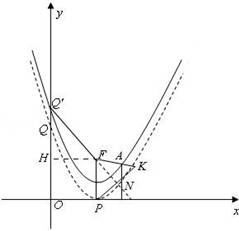
∴AN=y0﹣n,其中y0>n,
连接FP,
∵F(1,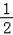 ),P(1,0),
),P(1,0),
∴FP⊥x轴,
∴FP∥AN,
∴∠ANF=∠PFN,
连接PK,则直线Q′F是线段PK的垂直平分线,
∴FP=FK,有∠PFN=∠AFN,
∴∠ANF=∠AFN,则AF=AN,
根据勾股定理,得,AF2=(x0﹣1)2+(y0﹣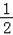 )2,
)2,
∴(x0﹣1)2+(y0﹣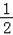 )2=(x
)2=(x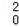 ﹣2x0+
﹣2x0+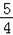 )+y
)+y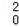 ﹣y0=y
﹣y0=y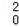 ,
,
∴AF=y0,
∴y0=y0﹣n,
∴n=0,
∴N(x0,0),
设直线Q′F的解析式为y=kx+b,
则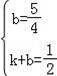 ,
,
解得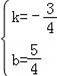 ,
,
∴y=﹣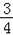 x+
x+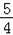 ,
,
由点N在直线Q′F上,得,0=﹣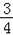 x0+
x0+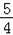 ,
,
∴x0=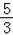 ,
,
将x0=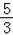 代入y0=x
代入y0=x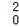 ﹣2x0+
﹣2x0+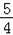 ,
,
∴y0=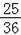 ,
,
∴A(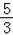 ,
,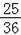 )
)
该题为二次函数综合题.
 浙公网安备33052302000911号
浙公网安备33052302000911号